Задания ВПР по математике за 5 класс с ответами за 2025 год (комплект 1)

Здесь представлены 2 варианта ВПР по математике за 5 класс с ответами за 2025 год из Комплекта заданий №1. Ознакомиться со всеми вариантами из остальных комплектов ВПР по математике за 5 класс за 2025 год можно на странице по ссылке.

Задания ВПР по математике за 5 класс, комплект 1, вариант 1

1. Приведите пример двузначного числа, большего 12, которое делится на 12 и не делится на 8.

Ответ: 36, 60, 84

2. Представьте число 4 в виде дроби со знаменателем 7.

Ответ: 28/7

ИЛИ

Представьте в виде обыкновенной дроби выражение 2/7 + 3/7.

Ответ: 5/7

ИЛИ

Представьте в виде обыкновенной дроби смешанное число 2 целых 3/8.

Ответ: 19/8

3. Выберите и запишите в ответ наибольшее из чисел: 9,8; 10,14; 10,3; 9,4.

Ответ: 10,3

4. В автобусе 51 место для пассажиров. Две трети этих мест уже заняты. Сколько ещё пассажиров может занять оставшиеся места?

Ответ: 17

5. Какое число надо вставить в окошко, чтобы равенство стало верным? ⬜ : 31 = 26

Ответ: 806

6. Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?

Запишите решение и ответ.

Решение: 
72 / 3 = 24
120 / 24 = 5

Ответ: 5 минут

7. Сколько роз нужно добавить к 186 розам, чтобы из этих цветов можно было составить букеты из 7 роз?

Ответ: 3 розы

8. В магазине зимой куртка продавалась по цене 8000 руб. Летом на куртки стала действовать скидка 20%. Сколько рублей составляет скидка?

Ответ: 1600 руб.

9. Найдите значение выражения 480480 : 24 − 4⋅(81−63) : 2.

Запишите решение и ответ.

Решение:

480480 : 24 − 4⋅(81−63) : 2 = 20020 – 4⋅18:2 = 20020 – 36 =

Ответ: 19984

10. В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Какова наименьшая цена за килограмм творога?

Запишите решение и ответ.

Решение:
Переводим цены в стоимость за килограмм:
1) 52 / 200 ⋅ 1000 = 52 ⋅ 5 = 260
2) 62 / 250 ⋅ 1000 = 62 ⋅ 4 = 248
3) 125 / 500 ⋅ 1000 = 125 ⋅ 2 = 250
4) 85 / 200 ⋅ 1000 = 85 ⋅ 5 = 425

Ответ: 248 руб.

11. На диаграмме представлены площади нескольких озёр. Пользуясь диаграммой, ответьте на вопросы.

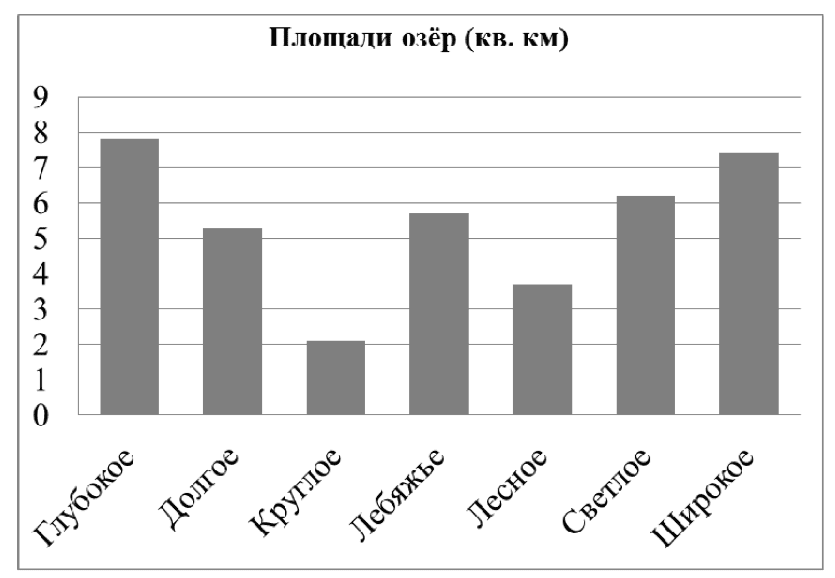
1) Какое озеро занимает третье место по величине площади среди представленных на диаграмме?

Ответ: Светлое

2) Площади двух из представленных озёр различаются вдвое. Какие это озёра?

Ответ: Лесное и Широкое

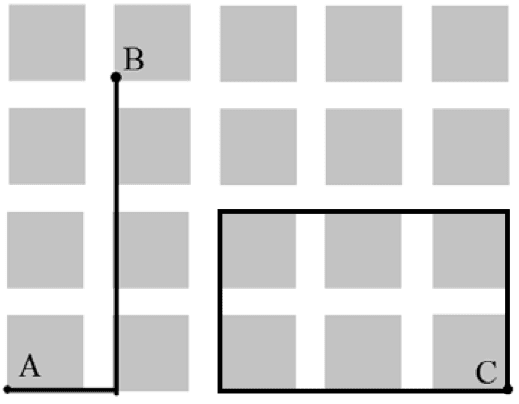
12. На плане одного из районов города клетками изображены кварталы, каждый из которых имеет форму квадрата со стороной 100 м. Ширина всех улиц в этом районе – 30 м.

1) Найдите длину пути от точки А до точки В, изображённых на плане.

Ответ: 520

2) Изобразите на плане маршрут, который начинается и заканчивается в точке С и имеет длину не меньше 1 км и не больше 1 км 200 м.

Ответ:

13. Из одинаковых кубиков сложили фигуру, а затем положили на неё сверху ещё две такие же фигуры из кубиков (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).

Рис. 1 Рис. 2 Из скольких кубиков состоит фигура, изображённая на рис. 2?

Ответ: 35

14. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на участке рядом с домом. Если укладывать в ряд по 10 плиток, то для квадратной площадки плиток не хватит. При укладывании по 8 плиток в ряд остаётся один неполный ряд, а при укладывании по 9 плиток тоже остаётся неполный ряд, в котором на 6 плиток меньше, чем в неполном ряду при укладывании по 8. Сколько всего плиток осталось после строительства дома?

Запишите решение и ответ.

Решение:
x — количество плиток
x < 10 ⋅ 10 = 100 (плиток меньше 100)
При укладывании по 8 плиток в неполном ряду может быть только 7 плиток, т.к. при укладывании по 9 плиток получается неполный ряд, в котором на 6 плиток меньше. То есть 1 плитка.
Теперь нужно найти такое число меньше 100, которое при делении на 8 даёт остаток 7, а при делении на 9 — остаток 1.
x : 8 = y (остаток 7)
x : 9 = z (остаток 7 — 6 = 1)
Путем перебора находим:
55:8 = 6 (остаток 7)
55:9 = 6 (остаток 1)

Ответ: 55

Задания ВПР по математике за 5 класс, комплект 1, вариант 2

1. В записи чётного трёхзначного числа каждая из цифр 1, 6 и 5 встречается один раз. Запишите наибольшее такое число.

Ответ: 516

2. Представьте число 7 в виде дроби с числителем 49.

Ответ: 49 / 7

3. Выберите и запишите в ответ наибольшее из чисел:

• 20,2
• 19,87
• 20,41
• 19,69

Ответ: 20,41

4. В вагоне электропоезда 56 мест для сидения, три четверти мест занято. Сколько свободных мест в вагоне?

Ответ: 14

5. Какое число надо вписать в окошко, чтобы равенство стало верным?

⬜ : 45 = 15

Ответ: 675

6. Варя утром вышла из дома и пошла в школу со скоростью 60 метров в минуту. Через 2 минуты вслед за ней вышел её брат Коля со скоростью 90 метров в минуту. Через несколько минут Коля догнал Варю. Через сколько минут Коля догнал Варю?

Запишите решение и ответ.

Решение:
Перед выходом Коли Варя прошла 60*2=120 метров
Если систему отсчета перенести на Колю, то относительно него Варя двигалась ему навстречу со скоростью 90-60=30 метров/минута
Расстояние в 120 метров при скорости сближения 30 будет преодолено 120 / 30 = 4 минуты и они встретятся

Ответ: 4 минуты

7. У Бори есть конструктор, из деталей которого можно собрать вертолёты. Чтобы собрать один вертолёт, нужно 16 винтиков и ещё другие детали. В конструкторе всего 110 таких винтиков. Какое наибольшее число вертолётов сможет собрать Боря, если других деталей хватает?

Ответ: 6

8. За первый час спортсмен пробежал 8910 метров, что составляет 30% всей дистанции. Найдите длину всей дистанции.

Ответ дайте в метрах.

Ответ: 29 700 

9. Найдите значение выражения (3090 − 223) ⋅14 + 4140 :15.

Запишите решение и ответ.

Решение:
(3090 − 223) ⋅ 14 + 4140 : 15 = 2867 ⋅ 14 + 276 = 40138 + 276 = 40414

Ответ: 40414

10. Нужно купить 60 кг стирального порошка. Данные о цене и массе стирального порошка в упаковке указаны в таблице. Сколько будет стоить самая дешёвая покупка? Ответ дайте в рублях.

Запишите решение и ответ.

Решение:
Переводим цены в стоимость за килограмм:
«Ариэль»: 645 / 6=107,5 р.
«Ромашка»: 1700 / 15 = 113,33 р.
«Аист»: 350 / 3 = 116, 67 р.
«Молекула»: 1520 / 10 = 152 р.
Итого самый дешевый — «Ариэль».
107,5 ⋅ 60 = 6450

Ответ: 6450 рублей

11. Чемпионаты мира по футболу проводятся с 1930 года. На диаграмме показано, сколько раз какая национальная сборная становилась чемпионом мира по футболу за период с 1930-го по 2019 год.

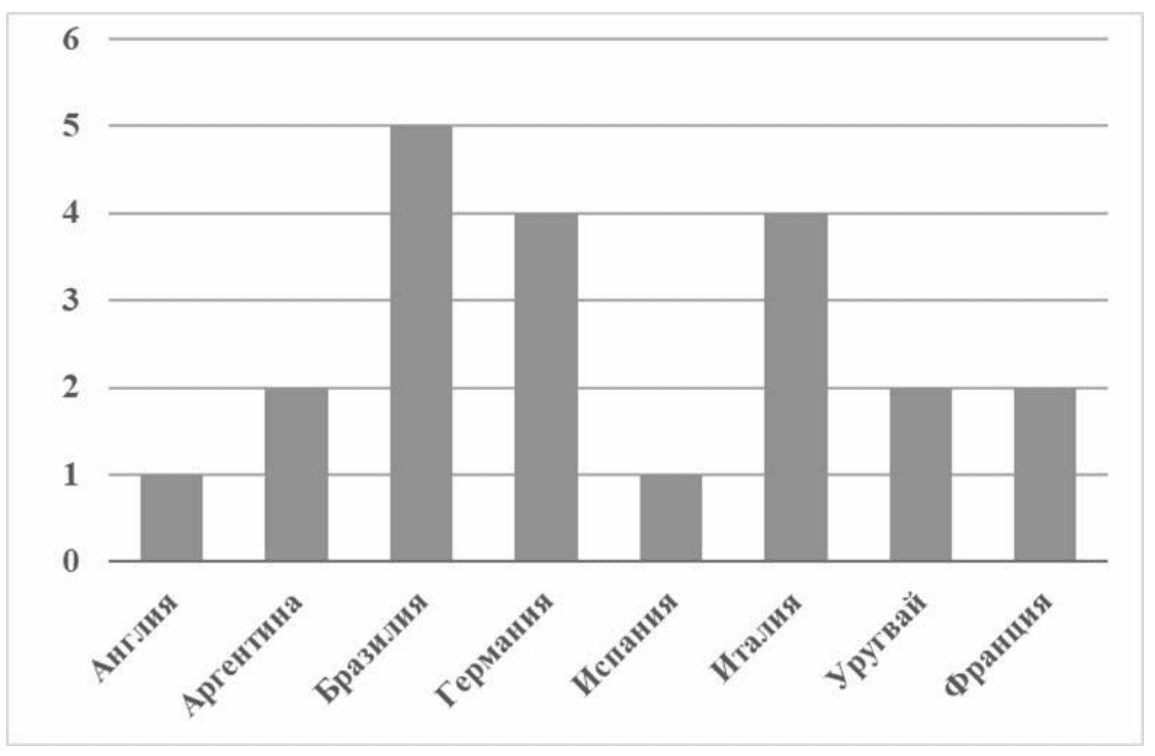
Пользуясь этими данными, ответьте на вопросы.

1) Сколько раз становилась чемпионом сборная команда Франции?

Ответ: 2

2) Сколько из представленных на диаграмме национальных сборных становились чемпионами больше трёх раз?

Ответ: Бразилия, Германия, Италия

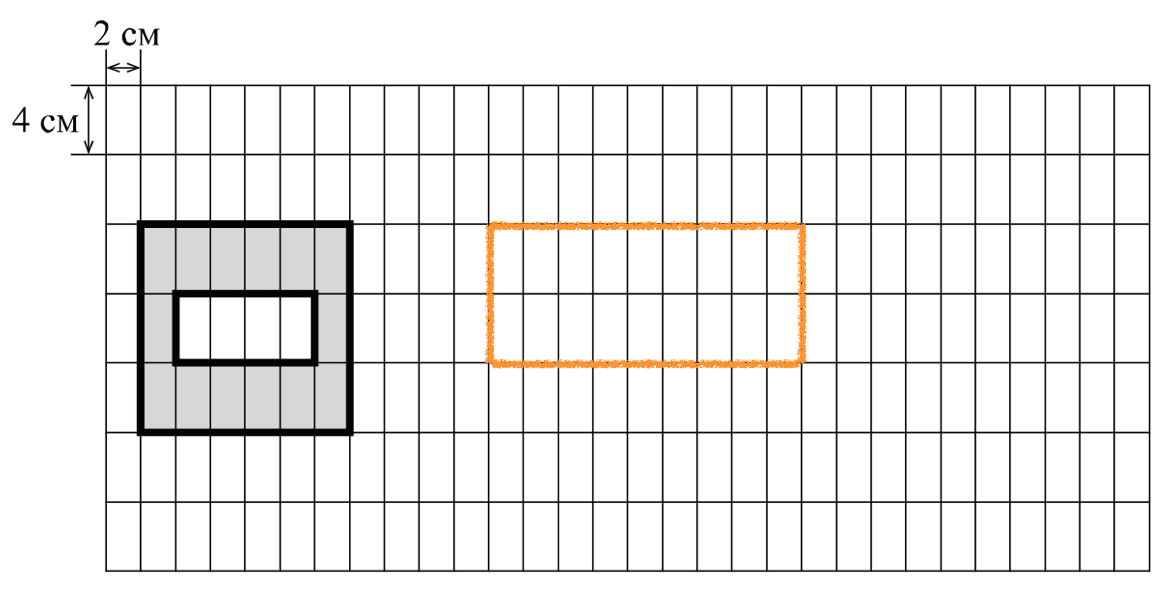
12. На рисунке дано поле, расчерченное на прямоугольники со сторонами 4 см и 2 см. На нём изображена фигура.

1) Найдите площадь закрашенной фигуры. Ответ дайте в квадратных сантиметрах.

Ответ: 112

2) На поле, данном в условии, начертите прямоугольник, площадь которого равна 144 см².

Ответ:

13. От деревянного бруска размером 30 см × 50 см × 90 см отпилили несколько дощечек размером 4 см × 30 см × 50 см. После этого остался брусок объёмом менее 4000 см³. Сколько дощечек отпилили?

Ответ: 22

14. В девяти аквариумах было поровну рыбок. Установили десятый аквариум, и рыбок расселили так, чтобы во всех аквариумах, кроме одного, их стало поровну, а в одном — на 1 больше, чем в каждом из остальных. Сколько всего было рыбок, если их было менее 100?

Запишите решение и ответ.

Решение:
Пусть:
x — рыбок в одном аквариуме (после пересадки)
y — рыбок всего

Тогда:
9⋅ x+ (x+1) = y или 10x + 1 = y
у < 100

Подставляем разные x, и смотрим, чтобы y был меньше 100 и при этом же делился на 9 без остатка:
Начнем с x=10. Тогда y=101 (слишком много рыбок)
Теперь возьмем x=9. Тогда y=91 (не делится на 9 без остатка)
Теперь возьмем x=8. Тогда y=81 (в самый раз)

Ответ: 81