Здесь представлены 2 варианта ВПР по математике за 7 класс с ответами за 2025 год из Комплекта заданий №1. Ознакомиться со всеми вариантами из остальных комплектов ВПР по математике за 7 класс за 2025 год можно на странице по ссылке.
Для быстрого перехода к нужному заданию используй поиск по странице (Ctrl+F) или нажми на соответствующий заголовок в Содержании!
Задания ВПР по математике за 7 класс, комплект 1, вариант 1
1. Найдите значение выражения \(\frac{5}{6} + \frac{7}{12} : \frac{7}{2} \).
2. Найдите значение выражения \(\frac{2,6 — 8,4}{2,5}\)
3. В таблице показано соответствие размеров женской обуви в России, Европейском союзе, Великобритании и США.

Покупательница носит туфли 37-го размера по российской системе. Какого размера туфли ей нужно спросить, если она зашла в обувной магазин во Франции?
4. Трактор едет по дороге, проезжая 10 метров за каждую секунду. Выразите скорость трактора в километрах в час.
5. Ежемесячная плата за телефон составляет 280 рублей в месяц. Сколько рублей составит ежемесячная плата за телефон, если она вырастет на 5%?
6. Катя младше Тани, но старше Даши. Ксюша не младше Даши. Выберите утверждения, которые верны при указанных условиях, и запишите в ответе их номера.
1) Таня и Даша одного возраста.
2) Среди названных четырёх девочек нет никого младше Даши.
3) Таня старше Даши.
4) Таня и Катя одного возраста.
7. На диаграмме показано содержание питательных веществ в овсяном печенье.
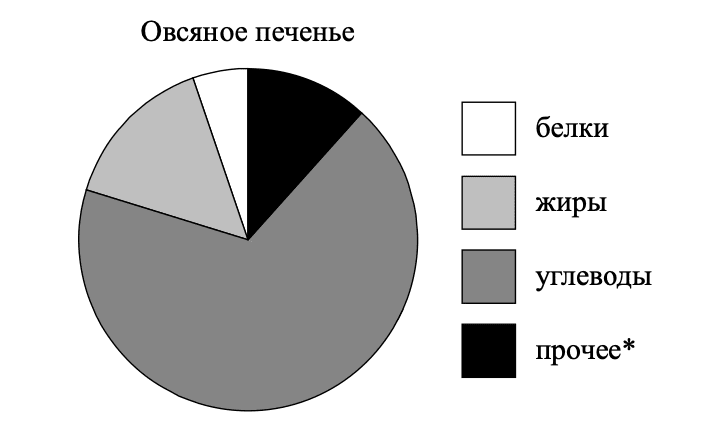
*К прочему относятся вода, витамины и минеральные вещества.
Определите по диаграмме, сколько примерно жиров содержится в 100 г овсяного печенья.
8. На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию.
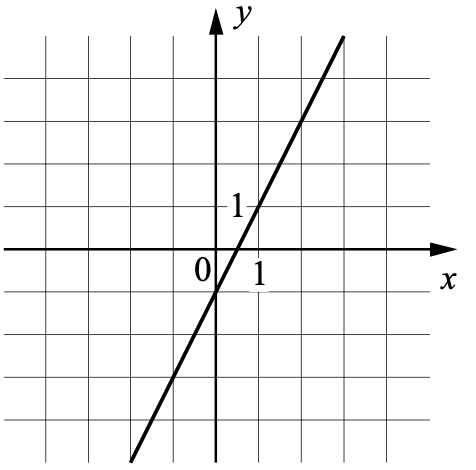
9. Решите уравнение \(2 + 3x = —2x —13\).
10. Прочтите текст.
Байкал — самое глубокое озеро на планете. Наибольшая глубина Байкала – 1642 метра. Байкал находится в Сибири между Иркутской областью и Республикой Бурятия. Живописные берега озера тянутся на 2000 километров, а площадь водной поверхности составляет 31 722 кв. км. Прибрежные территории отличаются уникальным разнообразием флоры и фауны. Вода в Байкале удивительно прозрачна: видно дно на глубине 40 метров. Запасы пресной воды в Байкале огромны: объём озера – 23 615 куб. км.
Байкал является частью огромной экологической системы, охватывающей сотни тысяч квадратных километров. Специалисты считают, что снижение уровня воды в Байкале даже на 10 см приведёт к необратимым катастрофическим последствиям для всей Восточной Сибири. Есть план построить на берегу озера завод, который будет выпускать байкальскую воду в бутылках. Экологи сильно обеспокоены сложившейся ситуацией.
Предположим, что завод будет выпускать 20 миллионов пятилитровых бутылок в год. Будет ли заметно понижение уровня воды в Байкале, вызванное деятельностью завода в течение трёх лет? Ответ обоснуйте.
20 млн. * 5 л. = 100 млн. литров/год или 100 тыс. куб.м/год или 0,0001 куб.км./год Площадь водной поверхности = 31722 кв.км., определим объём 10 см слоя: 31722*10/100/1000=3,1722 куб.км. За 3 года из озера минус 0,0003 куб.км., для необратимых последствий должно быть 3,1722 куб.км.
Ответ:
Понижение уровня воды в Байкале, вызванное деятельностью завода в течение трёх лет, не будет заметно (0,0003/31722 = 0.000000009457 км = 0,009457 мм — понижение уровня за 3 года).
11. Найдите значение выражения \((4 — y)^2 — y(y + 1)\) при \(y=\frac{1}{9}\).
12. Отметьте и подпишите на координатной прямой точки A (1,6), B \((-2\frac{}{})\) и С (−2,75).
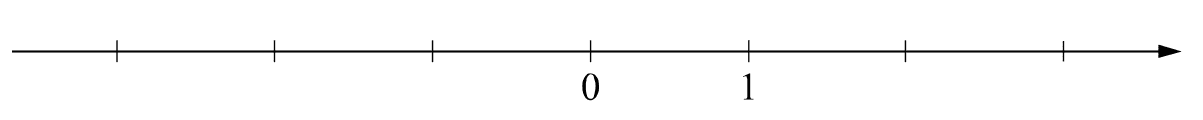
13. На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C . Найдите расстояние от точки A до прямой BC .
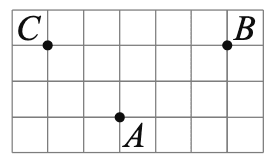
14. В треугольнике ABC проведена биссектриса CE. Найдите величину угла BCE, если∠BAC = 46° и ∠ABC = 78°.
Изобразим фигуру:
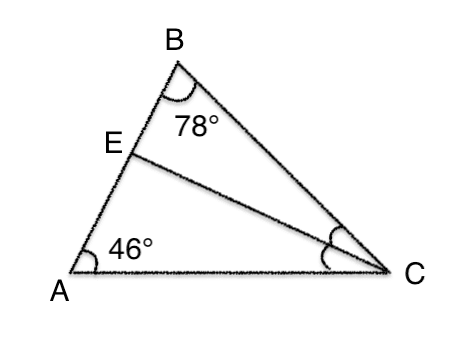
Мы видим, что два угла треугольника АВС нам известны. Можем найти величину угла С (АСВ) Сумма углов треугольника (любого) равна 180 градусов. Угол С равен: 180 — 46 — 78 = 56.
Поскольку условие задачи нам говорит, что СЕ — биссектриса, то углы ВСЕ и ЕСА — равны между собой. Значит, чтобы узнать величину угла ВСЕ нам нужно всего лишь разделить величину угла ВСА пополам.
56 : 2 = 28.
Ответ: Искомый угол ВСЕ равен 28 градусов.
15. Прочтите текст.
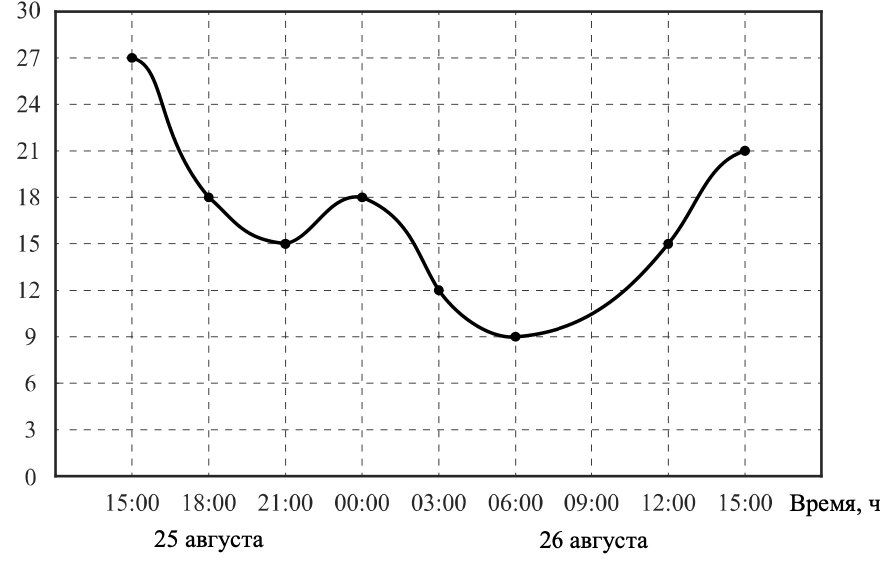
К трём часам дня 25 августа воздух прогрелся до +27°С, а затем температура начала быстро снижаться и за три часа опустилась на 9 градусов. Повеяло вечерней прохладой. Температура опускалась всё медленнее, и к девяти часам
вечера воздух остыл до 15°. К полуночи неожиданно потеплело на 3 градуса, но ветер снова сменил направление, и к 3 часам ночи температура воздуха опустилась до 12 градусов, а к восходу (в 6 часов утра)похолодало ещё на 3 градуса. Когда рассвело, воздух снова начал прогреваться, но такой жары, как накануне, 26 августа уже не случилось: в полдень было пасмурно, и термометры показывали всего 15°С, а в 15:00 температура оказалась на 6 градусов ниже, чем в это же время накануне.
По описанию постройте схематично график изменения температуры в течение суток с 15:00 25 августа до 15:00 26 августа.
16. Первый участок пути протяженностью 120 км автомобиль проехал со скоростью 80 км/ч, следующие 75 км — со скоростью 50 км/ч, а последние 110 км — со скоростью 55 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Запишите решение и ответ.
Всего автомобиль проехал 120 + 75 + 110 = 305 км. Найдем время на каждом участке пути:
120 : 80 = 1,5 ч
75 : 50 = 1,5 ч
110 : 55 = 2 ч
Общее время пути: 1,5+1,5+2 = 2 ч
Найдем среднюю скорость автомобиля на всем пути: 305/5 = 61 км/ч
Ответ: 61
Задания ВПР по математике за 7 класс, комплект 1, вариант 2
1. Найдите значение выражения \((\frac{17}{15}-\frac{1}{12})·\frac{20}{3}\).
2. Найдите значение выражения \(3.25 \cdot (-4.2 + 3.6)\) .
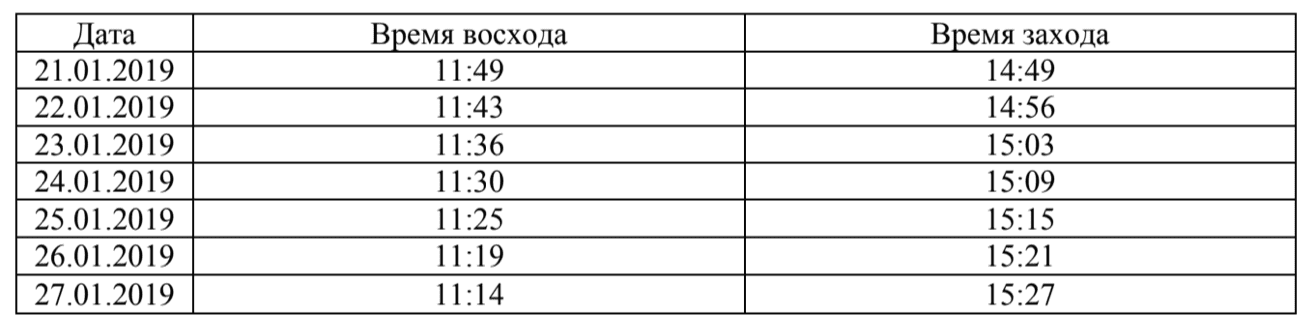
3. В таблице указано время восхода и захода солнца в Норильске с 21 января по 27 января 2019 года.
По данным таблицы определите долготу дня в Норильске 27 января 2019 года. Долгота дня (световой день) — время между восходом и заходом солнца.
4. Поезд проезжает 39 метров за каждую секунду. Выразите скорость поезда в километрах в час.
5. В период проведения акции цену на чайный сервиз снизили на 20%, при этом его цена составила 3200 рублей. Сколько рублей стоил сервиз до снижения цены?
6. Линейка стоит столько же, сколько точилка и карандаш вместе, а точилка дороже карандаша. Выберите верные утверждения и запишите в ответе их номера.
1) Точилка дороже линейки.
2) Две точилки стоят дороже линейки.
3) Карандаш дешевле линейки.
4) Точилка дешевле карандаша.
7. На диаграмме представлена информация о распределении продаж бытовой техники по разным типам торговых предприятий за последний год в некотором городе. Всего за указанный период было продано 400 000 единиц бытовой техники.
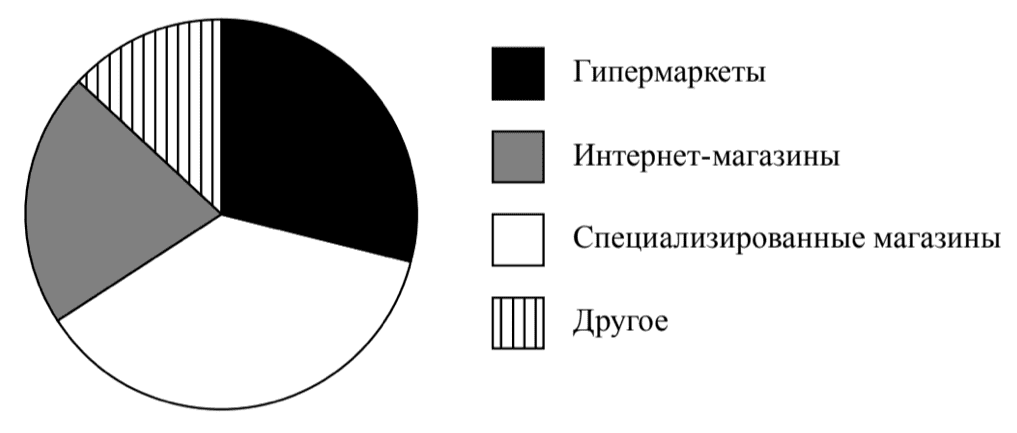
Определите по диаграмме, сколько примерно единиц бытовой техники было продано в специализированных магазинах.
8. График функции \(y=kx+4\frac{5}{7}\) проходит через точку с координатами \((14;–4\frac{2}{7})\). Найдите значение коэффициента k.
9. Решите уравнение x − 2 (3 x + 2) = 16.
10. Игорь работает в службе доставки интернет-магазина. Для упаковки коробок используется скотч. Он упаковал 400 маленьких коробок и израсходовал три рулона скотча полностью, а от четвёртого осталась ровно треть, при этом на каждую коробку расходовалось по 55 см скотча. Ему нужно заклеить скотчем 350 одинаковых коробок, на каждую нужно по 70 см скотча. Хватит ли четырёх целых таких рулонов скотча?
Запишите решение и ответ.
На маленькие коробки было израсходовано 400 · 55 = 22 000 см = 220 м скотча. При этом было израсходовано три рулона скотча полностью, а от четвёртого осталась ровно треть, т.е. израсходовано 3 и 2/3 рулона скотча.
\(3\frac{2}{3} = \frac{11}{3}\) или \(\frac{11}{3} х = 220\)
х=60 (метров скотча в 1 рулоне)
Сейчас на все коробки потребуется 350 · 70 = 24 500 см = 245 м. В четырёх рулонах 4 · 60 = 240 м скотча, поэтому скотча не хватит.
Ответ: 4 рулонов не хватит — не хватает 5 метров скотча
11. Найдите значение выражения \((n + 6)^2 + (2 — n)(2 + n)\) при \(n = -\frac{5}{12}\).
12. Отметьте и подпишите на координатной прямой точки A (4,69), B \((4\frac{9}{11})\) , C (−4,34).
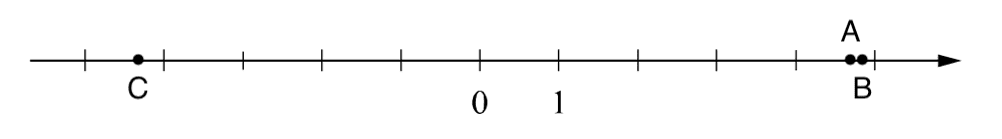
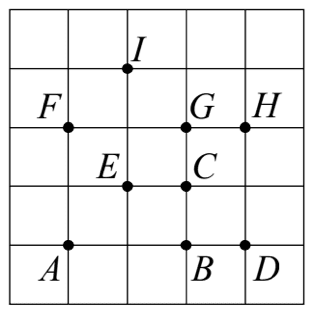
13. На клетчатой бумаге с размером клетки 1× 1 отмечено девять точек. Сколько из них удалено от прямой HD на расстояние 2?
14. В равнобедренном треугольнике ABC с основанием BC угол A равен 120°. Высота треугольника, проведённая из вершины B, равна 13. Найдите длину стороны BC. Запишите решение и ответ.
Нарисуем 2 треугольника:
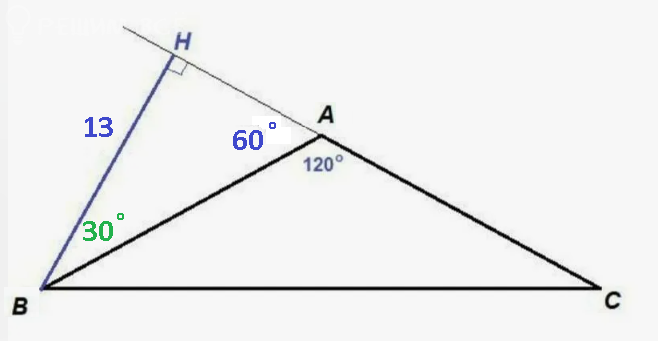
\(\sin(60^\circ) = \frac{AH}{AB}\)
Значит, \(AB = \frac{AH}{\sin(60^\circ)} = \frac{13}{\frac{\sqrt{3}}{2}} = \frac{26}{\sqrt{3}}\)
\(AB = AC\)
\(BC^2 = AB^2 + AC^2 — 2 \cdot AB \cdot AC \cdot \cos(120^\circ) =\)
\(=\left(\frac{26}{\sqrt{3}}\right)^2 + \left(\frac{26}{\sqrt{3}}\right)^2 — 2 \cdot \frac{26}{\sqrt{3}} \cdot \frac{26}{\sqrt{3}} \cdot \left(-\frac{1}{2}\right) = 3 \cdot \left(\frac{26}{\sqrt{3}}\right)^2\)
Ответ: 26
15. Прочитайте текст.
Цена на алюминий 23 января составляла 125 600 рублей за тонну. На следующий день цена выросла на 600 рублей, а затем снизилась на 1100 рублей. К открытию торгов 26 января цена за тонну составила 125 700 рублей. В субботу 27 января цена на алюминий вернулась к значению 23 января и оставалась без изменений до 28 числа включительно. К открытию торгов в понедельник 29 января цена за тонну резко снизилась на 1200 рублей, а следующие два дня цена росла на одно и то же количество рублей каждый день и 31 января достигла 126 400 рублей.
По описанию постройте график зависимости цены на алюминий (за тонну) от даты в течение девяти дней — с 23 января по 31 января. Точки соедините отрезками. Точка, показывающая цену алюминия 23 января, уже отмечена на рисунке.
16. Из пункта А в пункт В одновременно отправились велосипедист и пешеход. Скорость велосипедиста на 6 км/ч больше скорости пешехода. Найдите скорость велосипедиста, если время, которое затратил пешеход на дорогу из пункта А в пункт В, в два с половиной раза больше времени, которое затратил велосипедист на эту же дорогу.
Запишите решение и ответ.
Пусть скорость велосипедиста х км/ч. Тогда скорость пешехода (х − 6) км/ч. Поскольку пешеход затратил в два с половиной раза больше времени, чем велосипедист, чтобы преодолеть то же расстояние, его скорость в два с половиной раза меньше. Получаем уравнение:
2,5 · (x — 6) = x ⇒ 1,5x = 15 ⇒ x = 10
Ответ: 10 км/ч.
Ознакомиться со всеми вариантами из остальных комплектов ВПР по математике за 7 класс с ответами за 2025 год можно на этой странице >>