Если Вас интересует демоверсия ОГЭ по математике 2025 года, то Вы зашли «по адресу»! На этой странице Вы можете бесплатно скачать тренировочные варианты ОГЭ по математике 2024 г с ответами ФИПИ
Демоверсия ОГЭ по математике 2025
🔗 Скачать демоверсию ОГЭ по математике 2025 (PDF)
Ниже Вы можете просмотреть PDF-файл, не скачивая его.
Источник: https://fipi.ru/
Распечатай и реши ОГЭ 2025 математика
Готовишься к экзамену и хочешь практиковаться на реальных задачах? 📄 Мы собрали для тебя демоверсию ОГЭ 2025 по математике, которую можно скачать, распечатать и решать прямо на бумаге — как на самом экзамене. Такой формат помогает лучше понять структуру КИМов, научиться правильно распределять время и избежать типичных ошибок.
Нажмите на кнопку ниже, чтобы скачать PDF и начать подготовку:
🔗 Распечатай и реши ОГЭ 2025 математика (PDF)
Ниже мы приводим подробные пояснения по решению заданий с ответами. Это поможет Вам эффективно готовиться к ОГЭ, не видя все ответы под заданием, однако, имея возможность получить подробное пояснение по решению, если возникают затруднения с самостоятельным решением.
Решения и ответы к задачам демоверсии ОГЭ по математике 2025 года
1. Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.
Решение:
Из таблицы видно, что при диаметре 15 дюймов наименьшая ширина шины — 185 мм.
Ответ: 185
2. На сколько миллиметров радиус колеса с шиной маркировки 205/55 R14 больше, чем радиус колеса с шиной маркировки 165/65 R14?
Решение:
Радиус автомобильного колеса — это половина его диаметра. Формула радиуса:
\(
r = \frac{D}{2} = \frac{d + 2H}{2},
\)
где d — диаметр диска, а H — высота боковины шины.
Так как диск одинаков для обеих шин:
d = 14 × 25,4 = 355,6 мм
📏 Для шины 205/55 R14:
Найдём высоту боковины H₁:
\(
\frac{100 \cdot H_1}{B_1} = 55 \quad \Leftrightarrow \quad H_1 = \frac{55 \cdot B_1}{100} = \frac{55 \cdot 205}{100} = 112{,}75 \, \text{мм}
\)
📏 Для шины 165/65 R14:
Аналогично вычисляем H₂:
\(
\frac{100 \cdot H_2}{B_2} = 65 \quad \Leftrightarrow \quad H_2 = \frac{65 \cdot B_2}{100} = \frac{65 \cdot 165}{100} = 107{,}25 \, \text{мм}
\)
📐 Разность радиусов:
Находим разницу радиусов двух колёс:
\(
r_1 — r_2 = \frac{d + 2H_1}{2} — \frac{d + 2H_2}{2} = \frac{2H_1 — 2H_2}{2} = H_1 — H_2 = 5{,}5 \, \text{мм}
\)
Таким образом, при одинаковом диске, разница в радиусе шин 205/55 и 165/65 составляет 5,5 мм.
Ответ: 5,5 мм.
3. На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами 195/50 R15?
Решение:
Найдём общий диаметр колеса по формуле:
\(
D = d + 2H,
\)
где \( d \) — диаметр диска, а \( H \) — высота боковины. Оба параметра учитываются для расчёта полного диаметра.
🔹 Для шины 165/70 R13:
Диаметр диска:
\(
d_1 = 13 \cdot 25{,}4 = 330{,}2 \, \text{мм}
\)
Рассчитаем высоту боковины:
\(
\frac{100 \cdot H_1}{B_1} = 70 \quad \Leftrightarrow \quad H_1 = \frac{70 \cdot B_1}{100} = \frac{70 \cdot 165}{100} = 115{,}5 \, \text{мм}
\)
Тогда полный диаметр первого колеса:
\(
D_1 = d_1 + 2H_1 = 330{,}2 + 2 \cdot 115{,}5 = 561{,}2 \, \text{мм}
\)
🔹 Для шины 195/50 R15:
Диаметр диска:
\(
d_2 = 15 \cdot 25{,}4 = 381 \, \text{мм}
\)
Высота боковины:
\(
\frac{100 \cdot H_2}{B_2} = 50 \quad \Leftrightarrow \quad H_2 = \frac{50 \cdot B_2}{100} = \frac{50 \cdot 195}{100} = 97{,}5 \, \text{мм}
\)
Теперь находим полный диаметр второго колеса:
\(
D_2 = d_2 + 2H_2 = 381 + 2 \cdot 97{,}5 = 576 \, \text{мм}
\)
📐 Разница в диаметрах:
\(
D_2 — D_1 = 576 — 561{,}2 = 14{,}8 \, \text{мм}
\)
Ответ: При замене шин на 195/50 R15, диаметр колеса увеличится на 14,8 мм.
4. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
Решение:
Общий диаметр колеса вычисляется по формуле:
\(
D = d + 2H
\)
Рассмотрим шину с маркировкой 165/70 R13. Сначала определим диаметр диска:
\(
d = 13 \cdot 25{,}4 = 330{,}2 \, \text{мм}
\)
Теперь найдём высоту боковины шины:
\(
\frac{100 \cdot H}{B} = 70 \quad \Leftrightarrow \quad H = \frac{70 \cdot B}{100} = \frac{70 \cdot 165}{100} = 115{,}5 \, \text{мм}
\)
Подставим значения в формулу диаметра:
\(
D = d + 2H = 330{,}2 + 2 \cdot 115{,}5 = 561{,}2 \, \text{мм}
\)
Ответ: 561,2 мм.
5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами 175/60 R14? Результат округлите до десятых.
Решение:
При каждом обороте колесо проезжает путь, равный длине окружности, то есть
\( C = 2\pi r = \pi D \).
Найдём общий диаметр \( D = d + 2H \) для каждого комплекта шин.
Для шин с маркировкой 165/70 R13:
\( d_1 = 13 \cdot 25{,}4 = 330{,}2 \, \text{мм} \)
\( \frac{100 \cdot H_1}{B_1} = 70 \quad \Rightarrow \quad H_1 = \frac{70 \cdot 165}{100} = 115{,}5 \, \text{мм} \)
Значит, \( D_1 = d_1 + 2H_1 = 330{,}2 + 2 \cdot 115{,}5 = 561{,}2 \, \text{мм} \)
Теперь рассмотрим шины 175/60 R14:
\( d_2 = 14 \cdot 25{,}4 = 355{,}6 \, \text{мм} \)
\( \frac{100 \cdot H_2}{B_2} = 60 \quad \Rightarrow \quad H_2 = \frac{60 \cdot 175}{100} = 105 \, \text{мм} \)
Получаем \( D_2 = d_2 + 2H_2 = 355{,}6 + 2 \cdot 105 = 565{,}6 \, \text{мм} \)
Вычислим относительное увеличение расстояния за один оборот:
\(
\frac{\pi D_2 — \pi D_1}{\pi D_1} \cdot 100\% = \frac{565{,}6 — 561{,}2}{561{,}2} \cdot 100\% \approx 0{,}8\%
\)
Ответ: 0,8%
6. Представьте выражение \(\frac{3}{5} — \frac{2}{7}\quad\) в виде дроби со знаменателем 70. В ответ запишите числитель полученной дроби.
Решение:
Решаем выражение: \( \frac{3}{5} — \frac{2}{7} = \frac{3 \cdot 7}{5 \cdot 7} — \frac{2 \cdot 5}{7 \cdot 5} = \frac{21}{35} — \frac{10}{35} = \frac{11}{35} \)
Приводим дробь к знаменателю 70: \( \frac{11}{35} = \frac{11 \cdot 2}{35 \cdot 2} = \frac{22}{70} \)
Ответ: 22
7. Одно из чисел \(\frac{5}{9} ; \frac{11}{9}; \frac{13}{9};\frac{14}{9}\) отмечено на прямой точкой.
![]()
Какое это число?
\(\text{1)}\frac{5}{9}; \quad \text{2)} \frac{11}{9};\quad \text{3) }\frac{13}{9};\quad \text{3) }\frac{14}{9}\)
Ответ: 1)
8. Найдите значение выражения \( \frac{a^{14} \cdot (b^4)^3}{(a \cdot b)^{12}}\text{ при }a = 3 \text{ и } b = \sqrt{3}\).
Решение:
Решаем выражение: \(\frac{a^{14} \cdot (b^4)^3}{(a \cdot b)^{12}} = \frac{a^{14} \cdot b^{12}}{a^{12} \cdot b^{12}} = a^{14 — 12} = a^2 = 9\)
Ответ: 9
9. Решите уравнение \(2x^2− 3x + 1 = 0\).
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решение:
1) Сначала преобразуем выражение:
\( 2x^2 — 3x + 1 = 0 \quad \Leftrightarrow \quad 2x^2 — 3x = -1 \quad \Leftrightarrow \quad x^2 — \frac{3}{2}x = -\frac{1}{2} \)
2) Теперь попробуем довести до квадрата:
Добавим и вычтем квадрат половины коэффициента при \( x \):
\( x^2 — \frac{3}{2}x + \left(\frac{3}{4}\right)^2 — \left(\frac{3}{4}\right)^2 = -\frac{1}{2} \)
Сгруппируем первые три слагаемых как полный квадрат:
\( \left(x — \frac{3}{4}\right)^2 — \frac{9}{16} = -\frac{1}{2} \)
Переносим \( \frac{9}{16} \) направо:
\( \left(x — \frac{3}{4}\right)^2 = -\frac{1}{2} + \frac{9}{16} = \frac{1}{16} \)
3) Извлекаем корень:
\( x — \frac{3}{4} = \pm \frac{1}{4} \)
4) Находим два корня:
\( x = \frac{3}{4} + \frac{1}{4} = 1 \)
\( x = \frac{3}{4} — \frac{1}{4} = \frac{1}{2} \)
Ответ: 0,5
10. В магазине канцтоваров в продаже 100 ручек: 37 красных, 8 зелёных, 17 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка окажется красной или чёрной.
Решение задачи:
В магазине 100 ручек:
- 37 красных
- 8 зелёных
- 17 фиолетовых
- остальные — синие и чёрные поровну
Сначала найдём, сколько ручек уже учтено:
\( 37 + 8 + 17 = 62 \)
Значит, осталось:
\( 100 — 62 = 38 \)
Так как синих и чёрных поровну, то каждой по:
\( \frac{38}{2} = 19 \)
Теперь найдём, сколько ручек нас интересует (красные или чёрные):
\( 37 + 19 = 56 \)
И считаем вероятность:
\( P = \frac{56}{100} = 0.56 \)
Ответ: 0.56 или 56%.
11. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) \(y= −x^2 −x+ 5 \quad \) Б) \( y = -\frac{3}{4}x — 1 \quad\) В) \( y = -\frac{12}{x}\)
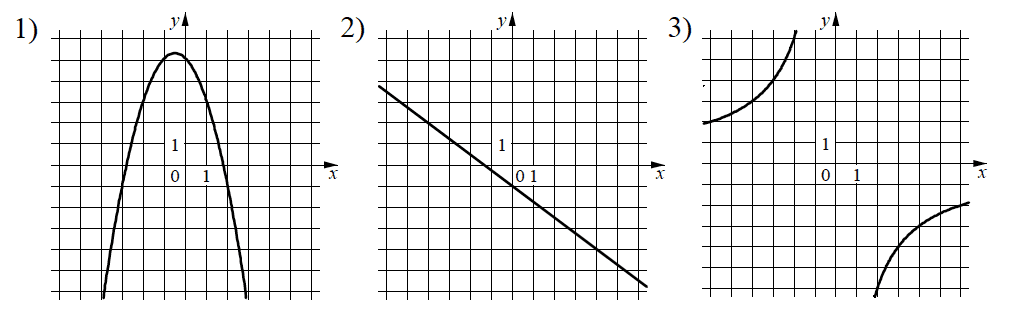
| А | Б | В |
|---|---|---|
Определяем характерные признаки у графиков функций:
А) \(y= −x^2 −x+ 5 \quad \) — здесь присутствует \(x^2 \), значит должна присутствовать парабола. Раз перед квадратом стоит минус, значит ветви будут смотреть вниз.
Б) \( y = -\frac{3}{4}x — 1 \) — простая линейная зависимость с отрицательным коэффициентом наклона 0,75 и сдвигом влево на 1.
В) \( y = -\frac{12}{x}\) — \(x\) в знаменателе означает, что это гипербола, а знак минус перед дробью, что ветви гиперболы лежат в четвертях II и IV
Ответ:
| А | Б | В |
|---|---|---|
| 1 | 2 | 3 |